基础概念
递归 是另外一个常见的基础语法。从语法上来说,在函数内部,调用自身就是递归 。
从编程思维上来说,递归是一种分治思维,将问题分解为规模更小的相同子问题 ,持续分解,直到问题规模足够小,能够被简单直接地解决。
例如,我们要计算 1, 2, 3, ..., 100
的和,我们用函数表示为 sum(100)
我们可以将问题分解为一个更小的相同子问题
-
sum(100)等价于:1, 2, 3,..., 99的和+ 100->sum(99) + 100 -
sum(99)等价于:1, 2, 3,..., 98的和+ 99->sum(98) + 99 -
sum(98)等价于:1, 2, 3,..., 97的和+ 98->sum(97) + 98 - ...
-
sum(3)等价于:1, 2的和+ 3->sum(2) + 3 -
sum(2)等价于:1的和 +2->sum(1) + 2 -
sum(1)等于1
我们可以从这个推论中得出一个重要公式:f(n) = f(n - 1) + n
所以到最后,当问题规模足够小的时候,我们可以直接解决它
1
function
sum
(
n
:
number
) {
2
if
(n
===
1
) {
3
return
1
4
}
5
// 调用自身
6
return
sum
(n
-
1
)
+
n
7
}
8
sum
(
100
)
// 5050
因此,我们发现,递归的本质是找到一种规律,让我们可以把一个大问题,拆分为一个或多个相同的小问题,直到问题规模足够小,能够直接解决。这是一种由大到小的编程思维
在执行过程中,递归分为两个阶段
- 递 :将原问题分解为若干个规模更小的子问题,直到问题足够小
- 归 :从最小问题开始,依次回归解决每个子问题,最终得到原问题的解
以 sum(5)
为例 ,我们用小一点的数来演示一下
10
// 递
20
入:
`sum(5)`
30
=>
`sum(4)`
+
5
40
=>
(
`sum(3)`
+
4
)
+
5
50
=>
((
`sum(2)`
+
3
)
+
4
)
+
5
60
=>
(((
`sum(1)`
+
2
)
+
3
)
+
4
)
+
5
70
// 归
80
=>
(((
1
+
2
)
+
3
)
+
4
)
+
5
90
=>
((
3
+
3
)
+
4
)
+
5
10
=>
(
6
+
4
)
+
5
11
=>
10
+
5
12
=>
15
递
的过程,不断分解问题,直到问题最小 sum(1)
归 的过程,从最小的问题开始解决,最终得到原问题的解。
执行过程在函数调用栈的表现形式如下
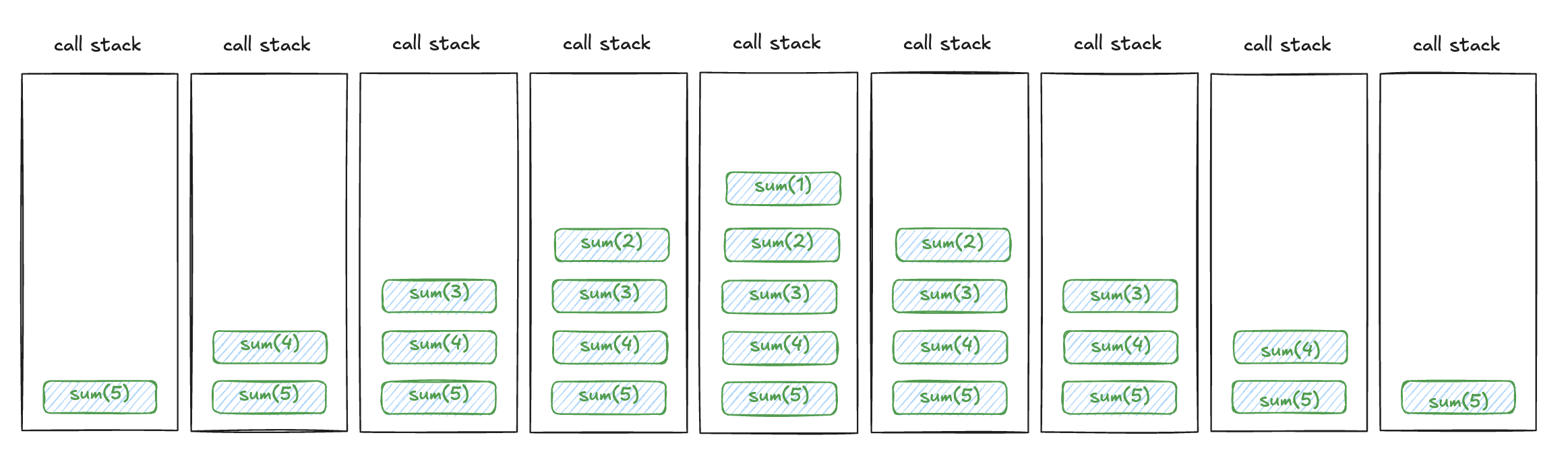
因此,在使用递归时,我们要关注两个显著的特征
- 1、自身调用 :原问题可以分解为子问题,子问题和原问题的求解方法是一致的,即都是调用自身的同一个函数
- 2、终止条件 :递归必须有一个终止的条件,即不能无限循环地调用本身
在利用递归思维解决问题时,我们也只需要关注这两个特征,找到规律和终止条件即可,我们来尝试利用递归问题来解决一些更复杂的逻辑
反转二叉树
原题地址:leetcode 226. Invert Binary Tree
给你一棵二叉树的根节点 root,翻转这棵二叉树,并返回其根节点。二叉树的每一个节点都格式如下所示
10
class
TreeNode
{
20
val
:
number
30
left
:
TreeNode
|
null
40
right
:
TreeNode
|
null
50
constructor
(
val
?:
number
,
left
?:
TreeNode
|
null
,
right
?:
TreeNode
|
null
) {
60
this
.val
=
(val
===
undefined
?
0
:
val)
70
this
.left
=
(left
===
undefined
?
null
:
left)
80
this
.right
=
(right
===
undefined
?
null
:
right)
90
}
10
}
1
function
invertTree
(
root
:
TreeNode
|
null
)
:
TreeNode
|
null
{
2
// ?
3
};
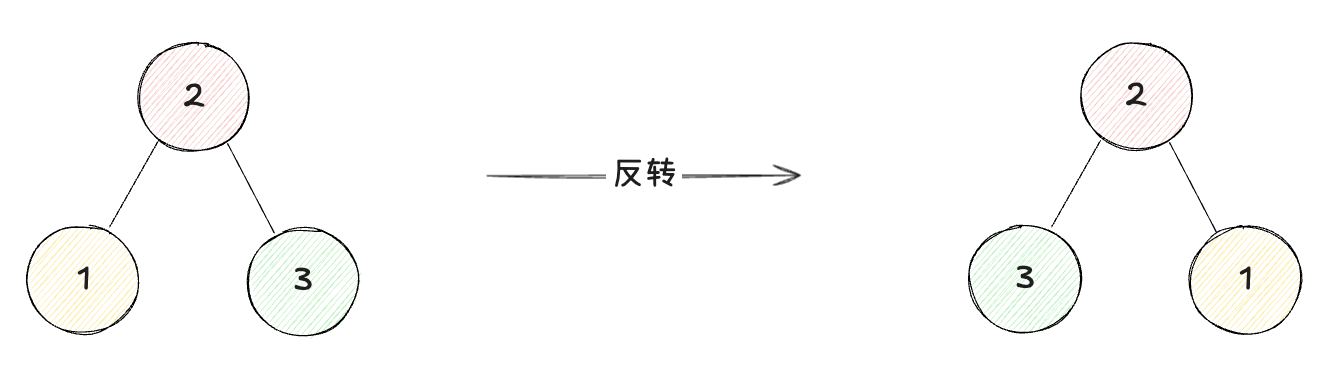
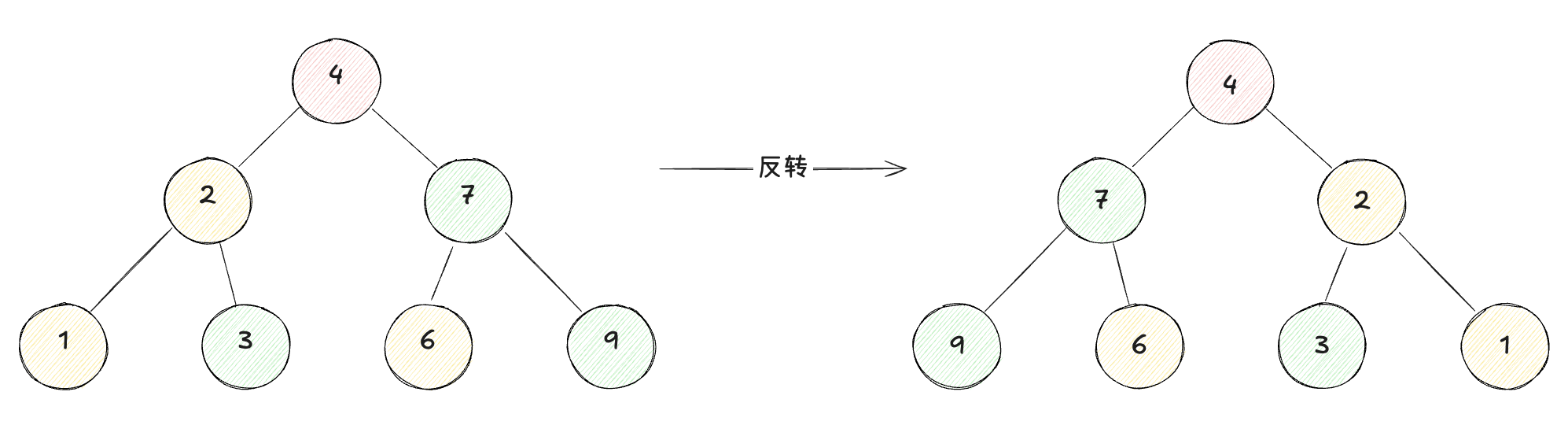
图例演示
题目解析
我们要翻转二叉树,其实就是交换每个节点的左右子树,因此,二叉树的每个节点都可以看做是一个子树的根节点。因此,我们可以利用递归来解决这个问题。
因此,找到的一个基本规律就是子节点的左右节点互换
1
// 利用了我们前面学习过的变量置换的技巧
2
const
left
=
root.left
3
root.left
=
root.right
4
root.right
=
left
带入到函数中来,那么上面的规律就是
1
root
->
invertTree
(root)
2
root.left
->
invertTree
(root.left)
3
root.right
->
invertTree
(root.right)
找到规律之后,我们还要找到终止条件,很明显,终止条件就是当节点没有任何子节点时,我们就无需进行交换操作了。由于我们在递归的过程中,还会把节点的左右子节点传入 invertTree
函数中,因此,终止条件就是当传入的节点为 null
时,我们就无需进行交换操作了。
1
if
(root
===
null
) {
2
return
root
3
}
最终答案如下
10
class
TreeNode
{
20
val
:
number
30
left
:
TreeNode
|
null
40
right
:
TreeNode
|
null
50
constructor
(
val
?:
number
,
left
?:
TreeNode
|
null
,
right
?:
TreeNode
|
null
) {
60
this
.val
=
(val
===
undefined
?
0
:
val)
70
this
.left
=
(left
===
undefined
?
null
:
left)
80
this
.right
=
(right
===
undefined
?
null
:
right)
90
}
10
}
11
12
export function
invertTree
(
root
:
TreeNode
|
null
)
:
TreeNode
|
null
{
13
if
(root
===
null
) {
14
return
root
15
}
16
// 利用前面学习的变量置换方法
17
const
left
=
invertTree
(root.left)
18
root.left
=
invertTree
(root.right)
19
root.right
=
left
20
return
root
21
};
记住,在复杂场景之下,我们不需要去在脑袋里面去具象递归的执行过程,只需要找到规律和终止条件即可。至于他到底如何执行,就让计算机自己去处理。如果你试图具象递归的过程,那么你就会认为递归是一个非常复杂的概念,这种思考方向是错误的。
斐波那契数列
所以,一切有固定规律的计算,我们都可以尝试用递归来解决。例如斐波那契数列。
斐波那契数列 是指这样一个数列:0,1,1,2,3,5,8,13,21,34,55,89 ... 这个数列从第 3 项开始 ,每一项都等于前两项之和。
用函数来表达这个规律就是
f
(n)
=
f
(n
-
1
)
+
f
(n
-
2
)
终止条件是
1
f
(
0
)
=
0
2
f
(
1
)
=
1
所以,我们可以用递归来实现这个函数,算出斐波那契数列的第 n 项
1
function
fib
(
n
:
number
)
:
number
{
2
if
(n
===
0
) {
3
return
0
4
}
5
if
(n
===
1
) {
6
return
1
7
}
8
return
fib
(n
-
1
)
+
fib
(n
-
2
)
9
}
爬楼梯
题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
题目解析
有的时候,找规律并没有那么容易,也比较烧脑。因此,我们在学习过程中,可以多做一些找规律的尝试。当然也可以直接覆盖所有题型来避免出现面试中无法快速找到规律的情况。
爬楼梯就是一个典型的,规律很难理解 的场景。
我们来尝试分一下。
由于目的地是第 n 阶,那么,我们可以有两种方式到达第 n 阶
-
第一种,从第 n - 1 阶,爬一步,到达第 n 阶,此时,到达第 n 阶的方法数,就是到达第 n - 1 阶的方法数,这种情况下
f(n) = f(n - 1)
比如,到达第 1 阶,只有一种方法,如果只允许我们爬一步 的话,到达第 2 阶,其实也只有一种办法。虽然多了一阶,但是到达的这一阶和到达前一阶方法数其实是一样的。
-
第二种,从第 n - 2 阶,爬两步,到达第 n 阶,此时,到达第 n 阶的方法数,就是到达第 n - 2 阶的方法数,这种情况下
f(n) = f(n - 2)
结合起来考虑,最终的规律就是
1
// 当我们可以爬 1 阶或者 2 阶时
2
f
(n)
=
f
(n
-
1
)
+
f
(n
-
2
)
大家尝试一下看看能不能理解,如果短时间内无法理解,就直接记住这个情况即可。
接下来就是终止条件了。
-
当只有 0 阶时,直接到达终点,我们设置默认值为 1,因此,
f(0) = 1 -
当只有 1 阶时,我们只有一种方法,就是爬 1 阶,因此,
f(1) = 1
1
function
climbStairs
(
n
:
number
)
:
number
{
2
if
(n
===
0
) {
3
return
1
4
}
5
if
(n
===
1
) {
6
return
1
7
}
8
return
climbStairs
(n
-
1
)
+
climbStairs
(n
-
2
)
9
};
爬楼梯,实际上就是一个斐波那契数列
递归思维是我们在后续的学习过程中最重要的思维方式之一。虽然在某些场景下不会再语法上使用递归。但开发思维依然是递归那一套。
递归的弊端在某些场景下执行效率不算高,并且存在栈溢出的风险。因此在实践中我们要根据具体情况来选择是否使用递归。
思考题:二叉树的最大深度
给定一个二叉树 root ,返回其最大深度。
二叉树的最大深度:是指从根节点到最远叶子节点的最长路径上的节点数。如下图所示的二叉树,最大深度为 3