请勿第一时间看答案,先自己思考,思考不出来,再看答案
思考题:平衡二叉树判断
题目描述
给定一个二叉树,判断它是否是平衡二叉树 .
平衡二叉树的定义:一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。
例如下面三个图例,前两个是平衡二叉树,最后一个不是平衡二叉树。
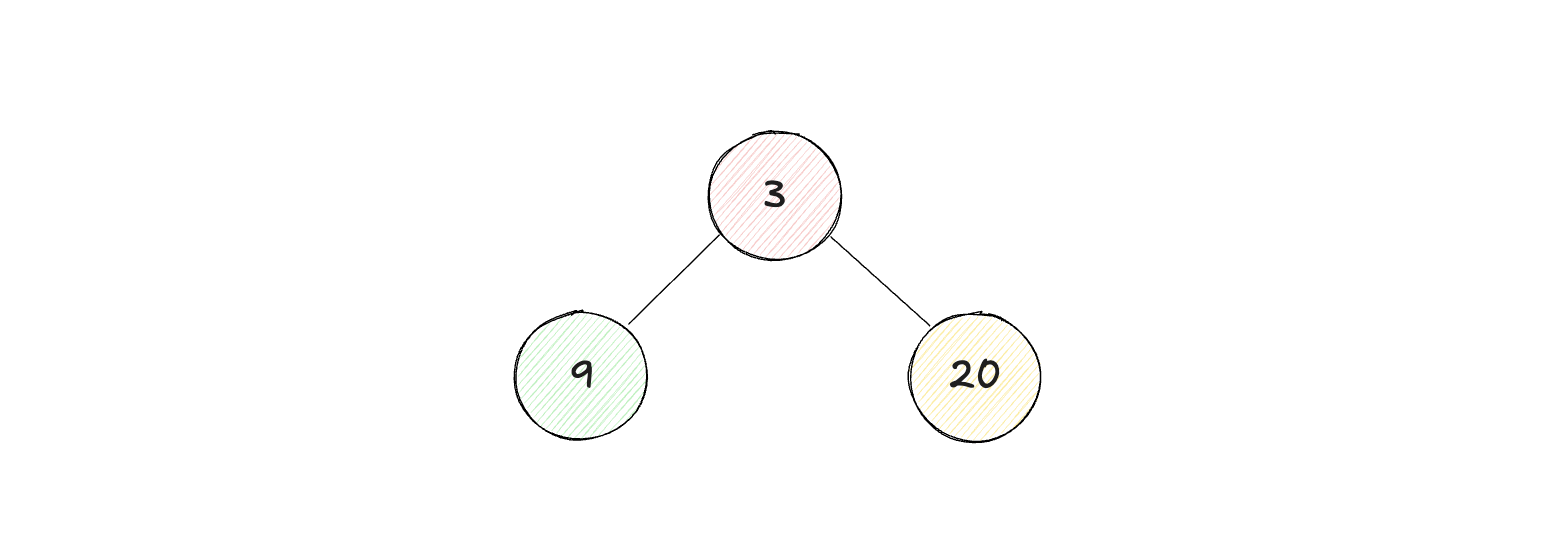
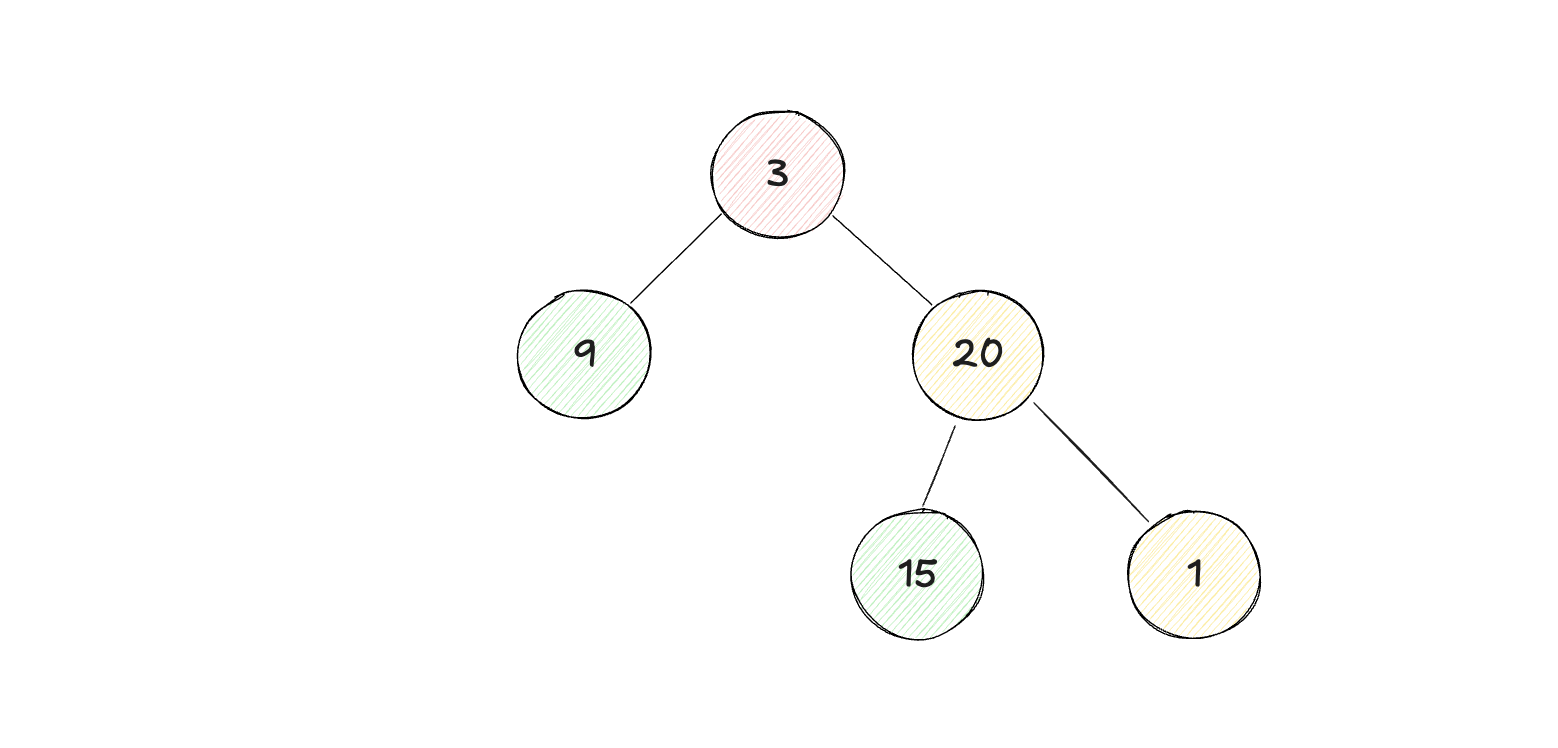
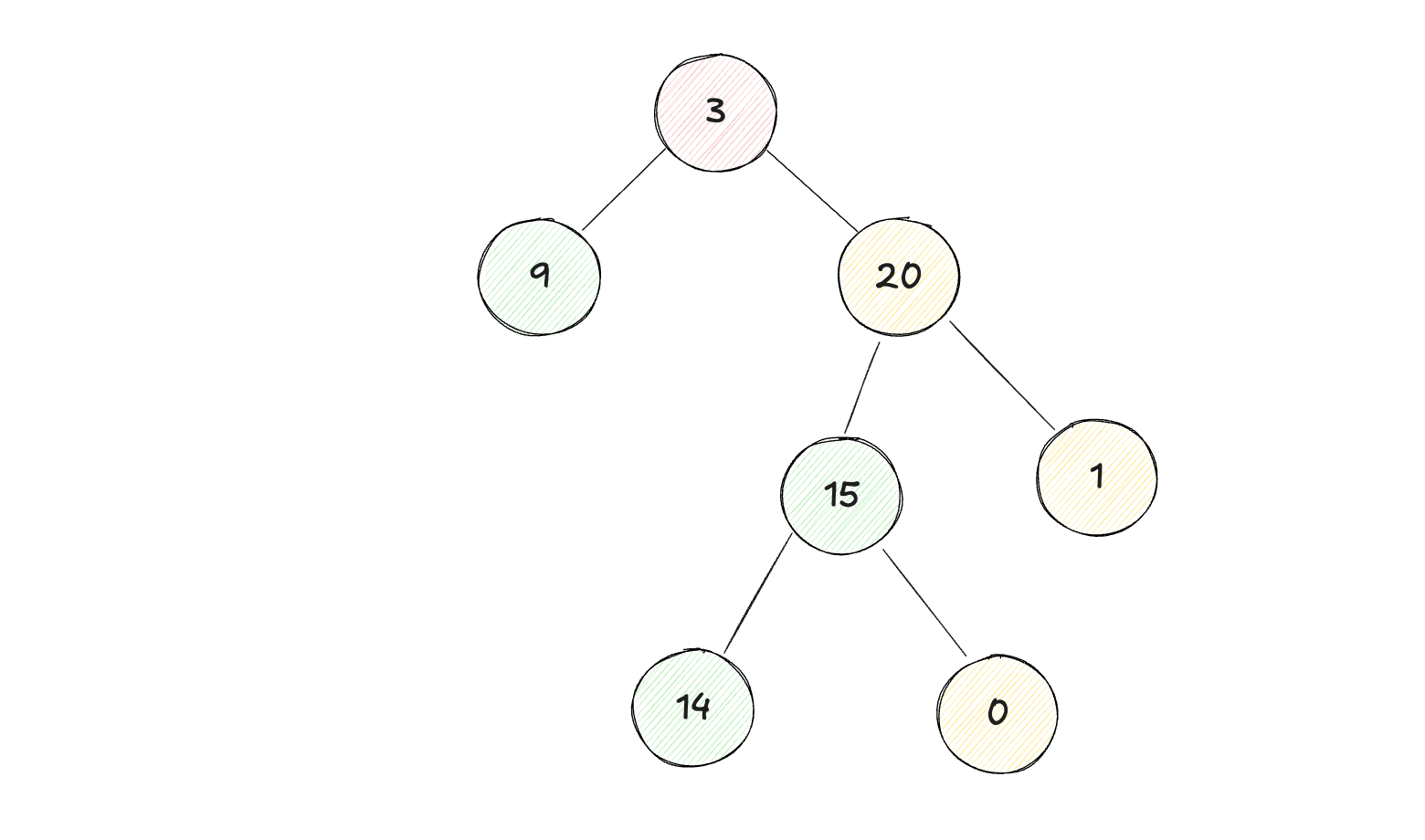
原题地址:leetcode 110
目前优先使用递归的思路来解答,如果对递归非常熟练,也可以使用其他新的思维来解答
解题思路
前面一个题,我们知道了如何去计算一个二叉树的最大深度,因此,如果我们要判断一棵树是否平衡,只需要利用上一题的结果,然后判断左右两个节点的深度差不超过 1 即可
我们先把上一题的答案拷贝过来
1
export function
maxDepth
(
root
:
TreeNode
|
null
)
:
number
{
2
if
(root
===
null
) {
3
return
0
4
}
5
return
Math.
max
(
maxDepth
(root.left),
maxDepth
(root.right))
+
1
6
};
然后通过判断一个节点的深度差即可
1
export function
isBalanced
(
root
:
TreeNode
|
null
)
:
boolean
{
2
if
(root
===
null
) {
3
return
true
4
}
5
const
leftDepth
=
maxDepth
(root.left)
6
const
rightDepth
=
maxDepth
(root.right)
7
8
return
Math.
abs
(leftDepth
-
rightDepth)
<=
1
9
}
不过我们还要注意一个细节,那就是,如果子树不平衡,那么整棵树也是不平衡的。因此,我们还需要递归的去判断子树是否平衡。
return
Math.
abs
(leftDepth
-
rightDepth)
<=
1
&&
isBalanced
(root.left)
&&
isBalanced
(root.right)
完整代码如下
answer.ts
10
class
TreeNode
{
20
val
:
number
30
left
:
TreeNode
|
null
40
right
:
TreeNode
|
null
50
constructor
(
val
?:
number
,
left
?:
TreeNode
|
null
,
right
?:
TreeNode
|
null
) {
60
this
.val
=
(val
===
undefined
?
0
:
val)
70
this
.left
=
(left
===
undefined
?
null
:
left)
80
this
.right
=
(right
===
undefined
?
null
:
right)
90
}
10
}
11
12
function
maxDepth
(
root
:
TreeNode
|
null
)
:
number
{
13
if
(root
===
null
) {
14
return
0
15
}
16
return
Math.
max
(
maxDepth
(root.left),
maxDepth
(root.right))
+
1
17
};
18
19
export function
isBalanced
(
root
:
TreeNode
|
null
)
:
boolean
{
20
if
(root
===
null
) {
21
return
true
22
}
23
const
leftDepth
=
maxDepth
(root.left)
24
const
rightDepth
=
maxDepth
(root.right)
25
26
return
Math.
abs
(leftDepth
-
rightDepth)
<=
1
&&
isBalanced
(root.left)
&&
isBalanced
(root.right)
27
}
28
专栏首页
到顶
专栏目录