题目描述
现有一个正整数数组,要求从该数组中,找出一个总和为目标值的连续子数组,输出该子数组的最大长度
技术要点:
- for 循环 或者 while 循环
- 双指针
- 滑动窗口/队列
解题思路一
利用滑动窗口的逻辑来解释
利用双指针,一个指针指向子数组的起始位置,命名为 start
,另一个指针指向子数组的结束位置,命名为 end
。由于子数组是连续的,因此可以通过移动指针来改变子数组的大小。
因此在有的地方,称这种类似的方法为滑动窗口。实际上准确的说法应该是队列
遍历数组的过程中,我们让 end
指针不断的向右移动,每次移动 end
指针时,都要计算 start
到 end
之间的元素之和。
当 start
到 end
之间的元素之和等于目标值 k
时,记录当前子数组的长度
如果 start
到 end
之间的元素之和大于目标值 k
,则表示需要减少元素以减少总和,此时则需要将 start
指针向右移动一位,直到 start
到 end
之间的元素之和小于等于目标值 k
。
代码如下所示
10
function
maxSubarrayLength
(
arr
,
k
) {
20
let
sum
=
0
;
30
let
maxLen
=
0
;
40
let
start
=
0
;
// 子数组的起始位置
50
60
// 定义子数组的结束位置,并不断地向右移动
70
for
(
let
end
=
0
; end
<
arr.
length
; end
++
) {
80
// 每移动一次,计算子数组的和
90
sum
+=
arr[end];
10
11
// 当子数组的和大于目标值时,需要移动子数组的起始位置,以减小子数组的和
12
while
(sum
>
k
&&
start
<=
end) {
13
sum
-=
arr[start];
14
start
++
;
15
}
16
17
// 当子数组的和等于目标值时,记录当前子数组的长度
18
if
(sum
===
k) {
19
maxLen
=
Math.
max
(maxLen, end
-
start
+
1
);
20
}
21
}
22
23
return
maxLen;
24
}
解题思路二
第二种思路是利用空间换时间的方式,可以得到更快的执行时间
首先,我们依然定义两个指针 start
和 end
,分别指向子数组的起始位置和结束位置。end
指针不断向右递增移动。
在移动 end
指针的过程中,我们需要记录从数组的第一个元素到 end
之间的元素总和 sum
,并将其存储在一个哈希表中。哈希表的键为元素总和,值为该元素总和对应的下标。
由于子元素的总和是已知的,因此我们可以通过判断哈希表中是否存在 sum - k
的键来确定是否存在一个子数组的总和等于 k
。公式如下图所示:
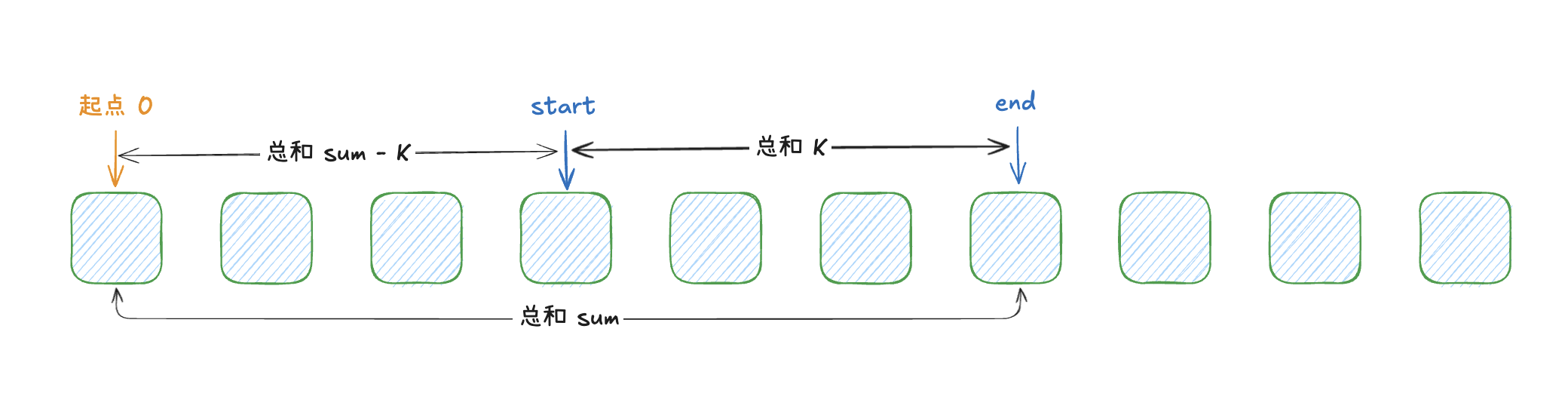
如果存在,我们可以通过计算 end - start
来得到当前子数组的长度,并将其与之前记录的最大子数组长度进行比较,取较大值作为新的最大子数组长度。
10
function
fn
(
arr
,
k
) {
20
let
maxLen
=
0
;
30
let
sum
=
0
;
40
const
map
= new
Map
();
50
map.
set
(
0
,
-
1
);
// 初始化哈希表,将 (0, -1) 键值对添加到哈希表中 (sum, index)
60
70
for
(
let
end
=
0
; end
<
arr.
length
; end
++
) {
80
sum
+=
arr[end];
90
if
(map.
has
(sum
-
k)) {
10
const
start
=
map.
get
(sum
-
k);
11
maxLen
=
Math.
max
(maxLen, end
-
start);
12
}
13
if
(
!
map.
has
(sum)) {
14
map.
set
(sum, end);
15
}
16
}
17
return
maxLen;
18
}