滑动窗口是在算法题中,经常提及的一个概念。他通常运用于特定长度的数组或者字符串等连续的线性数据结构上。
通常,我们会维护两个可移动 的指针,分别代表窗口的两个边界
1
// 左边界
2
let
left
=
0
;
3
// 右边界
4
let
right
=
0
;
这样在数组中,索引闭合区间
[left, right]
就代表了一个窗口
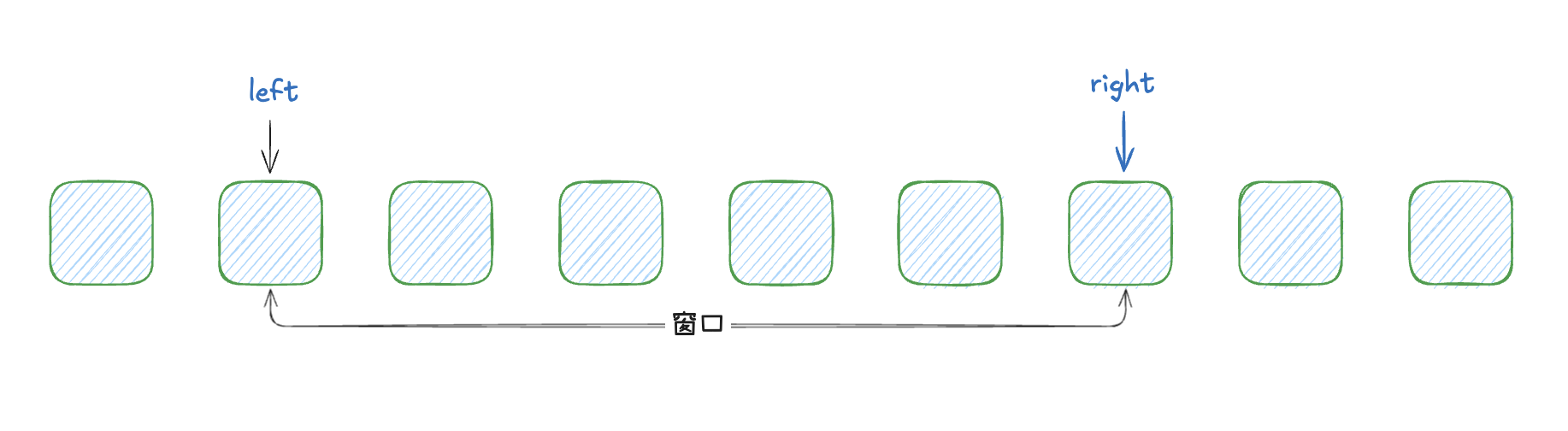
我们可以移动右边界来扩大窗口,移动左边界来缩小窗口。也可以同步移动左右边界来维持窗口的宽度不变。
一、案例讲解
现在有这样一个题目:从一个数组中,找出长度为 k
的连续子数组,要求返回所有子数组总和的最大值。
题目解析
由于需要找出长度为 k
的子数组,我们可以先固定窗口的左边界,让窗口的右边界移动,直到窗口的长度为 k
时,再同步移动左右边界。
在移动的过程中,我们可以维护一个变量 sum
来记录窗口内所有元素的总和,同时维护一个变量 max
来记录所有子数组总和的最大值。
此时需要注意的是,如果我们每次都循环去计算窗口内的子元素之和,会导致耗时过长。因此,我们可以利用滑动窗口的特性,每次移动窗口时,只需要将窗口内的元素总和减去左边界元素,再加上右边界元素即可。
如下图示可以表达指针的移动过程
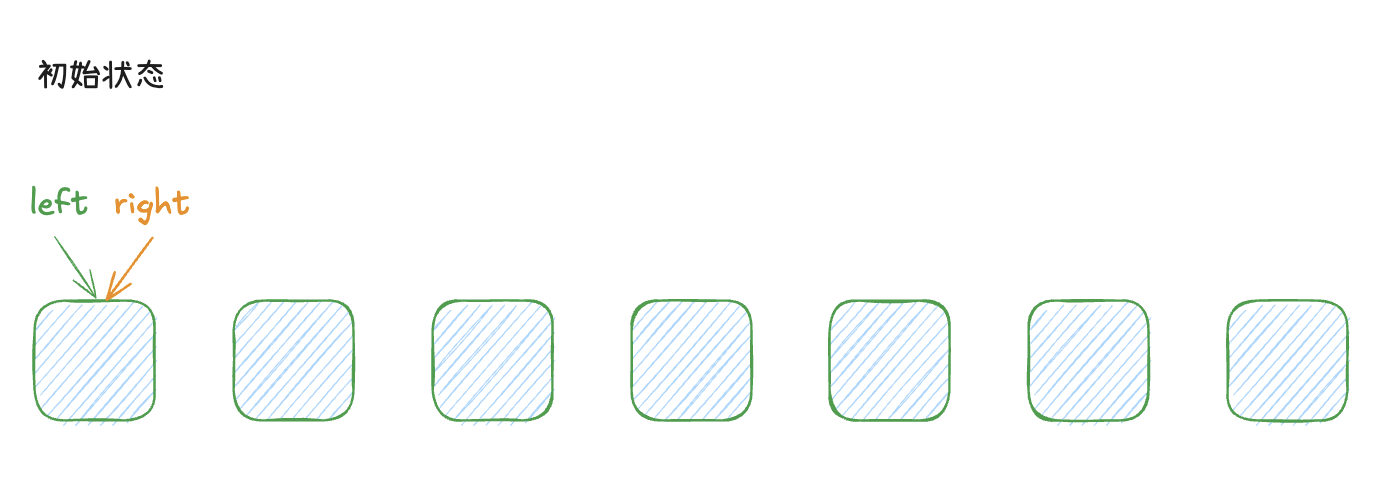
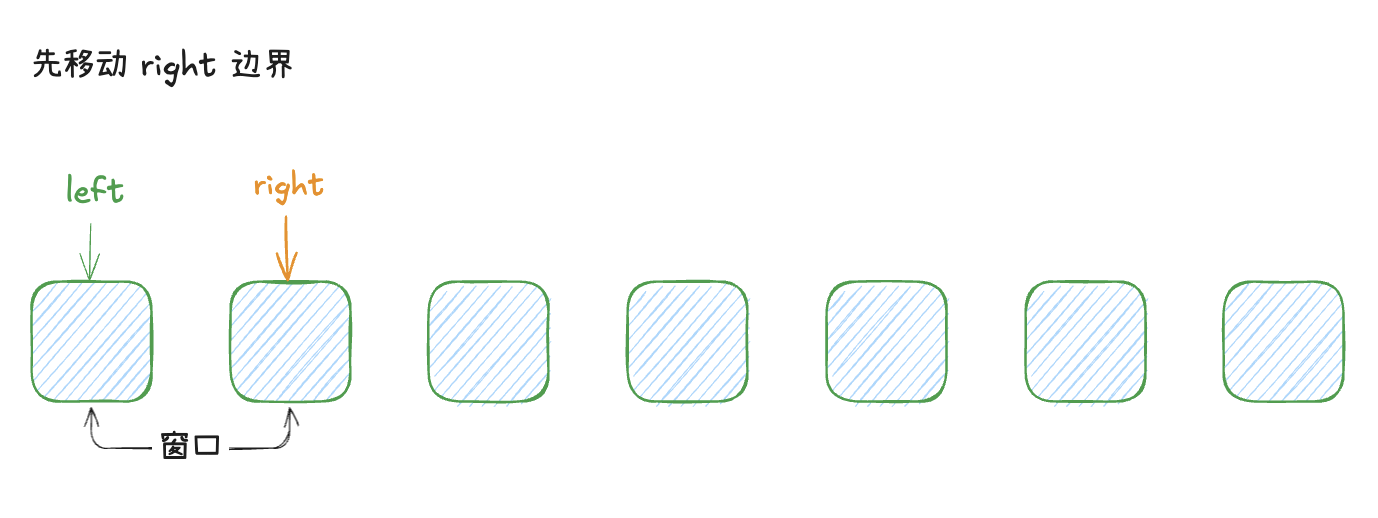
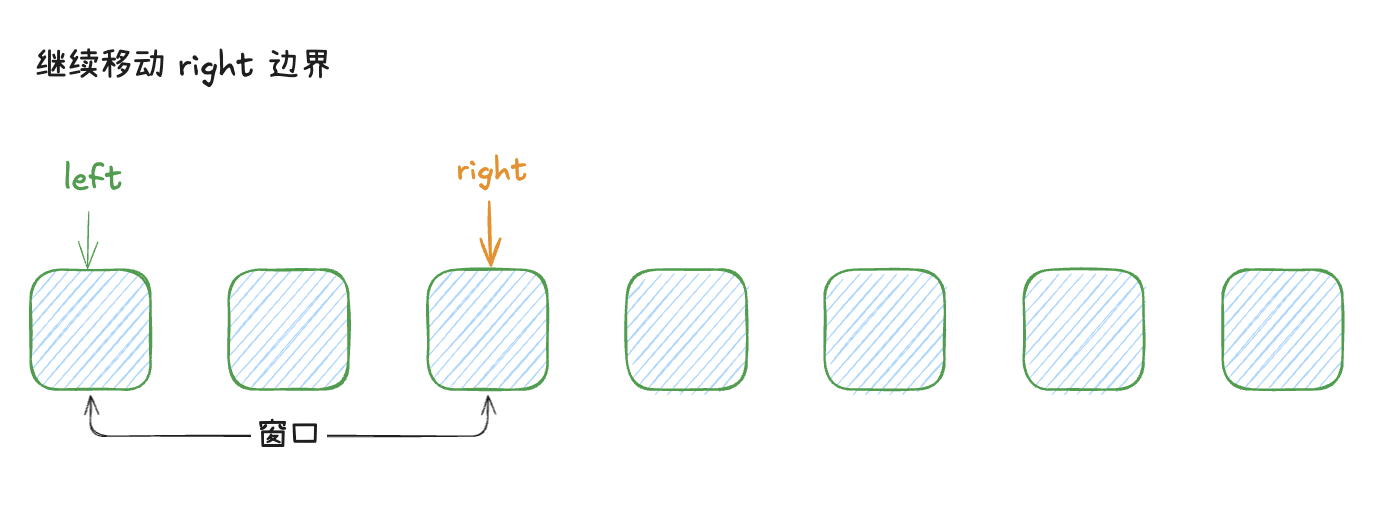
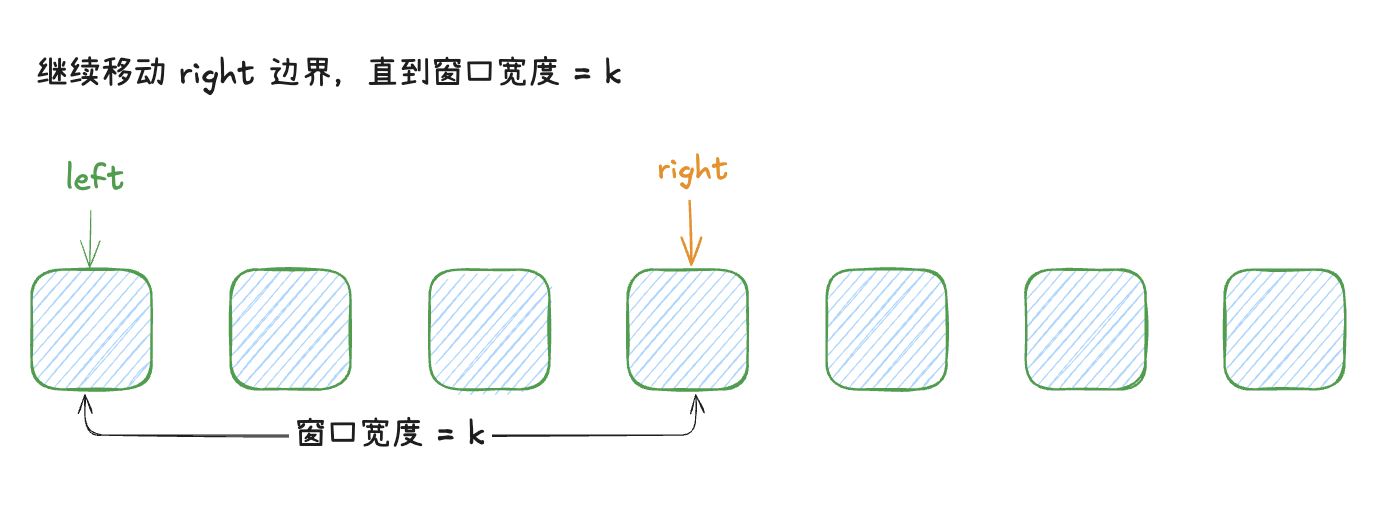
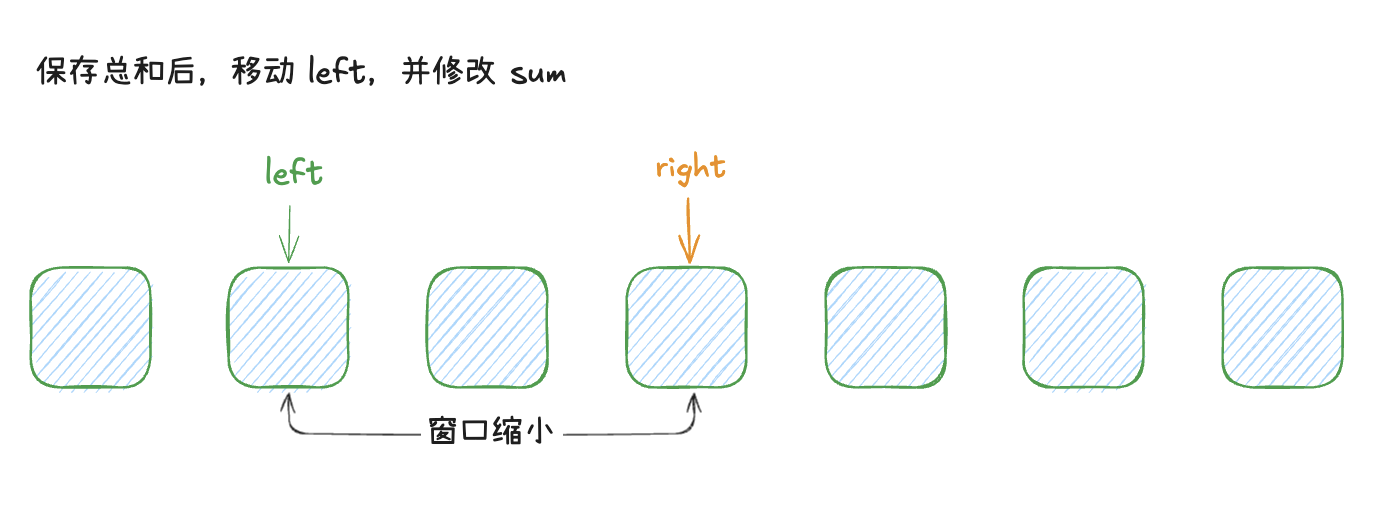
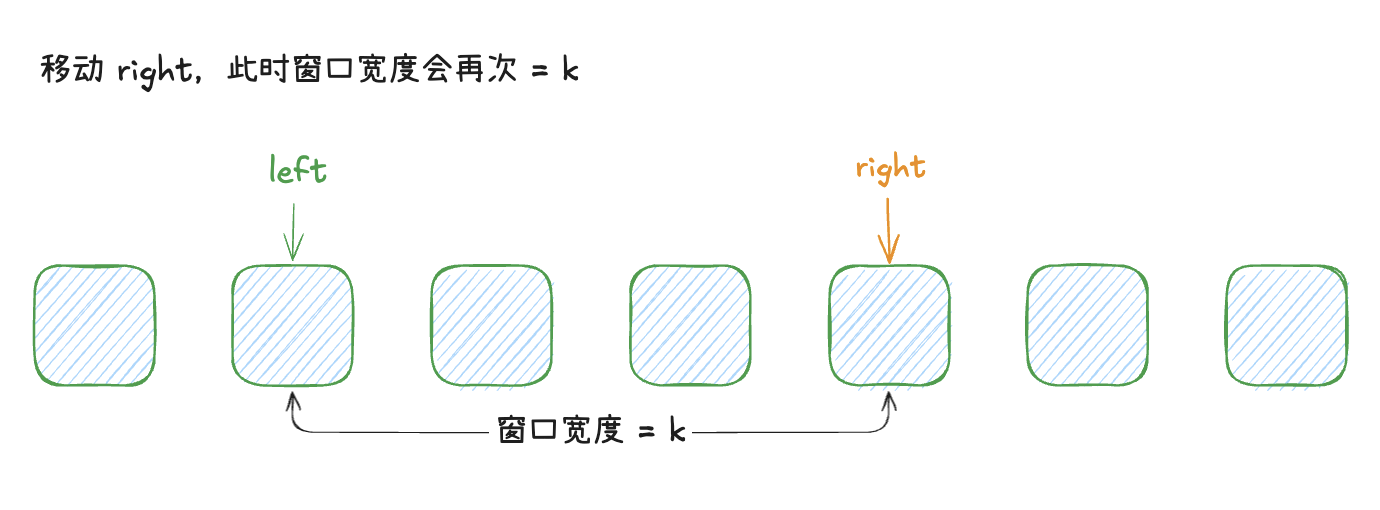
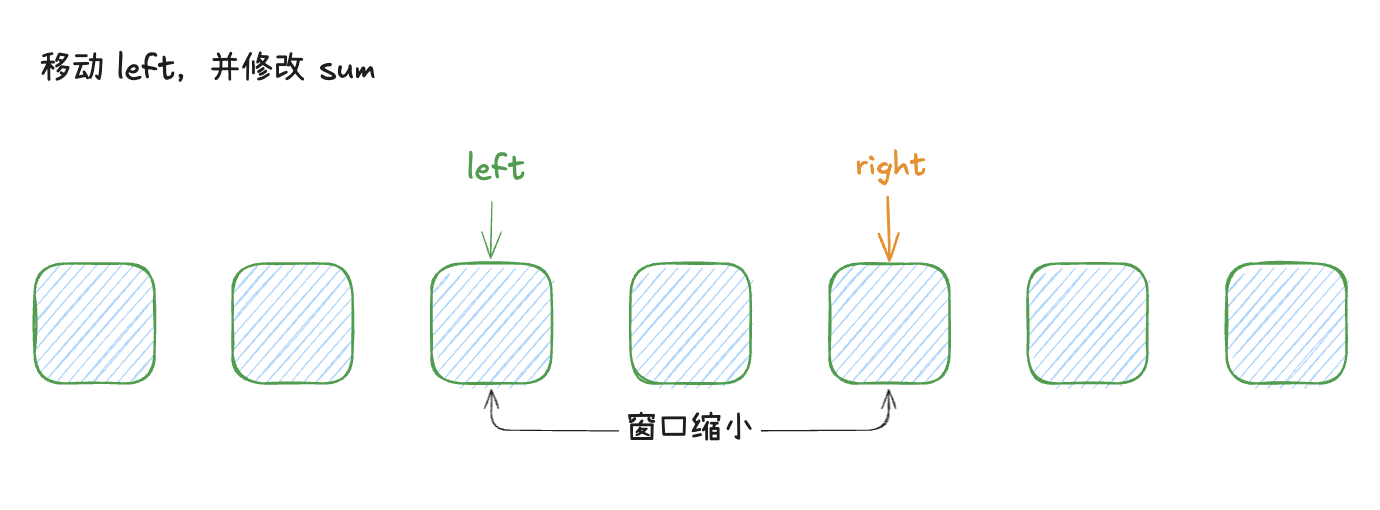
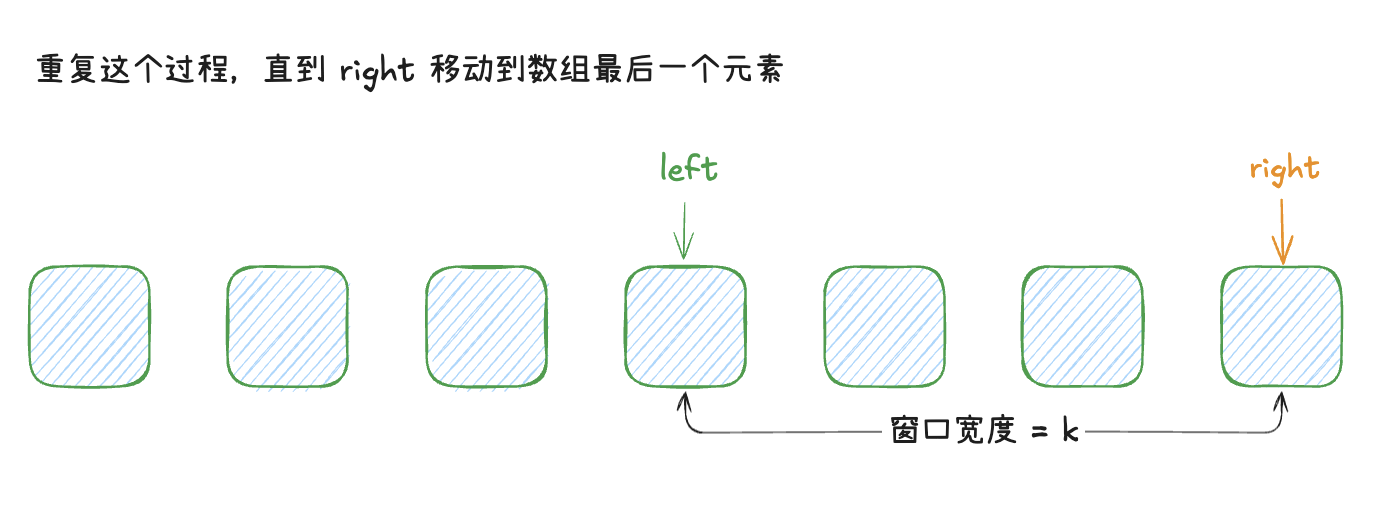
代码如下所示
10
export function
maxSum
(
arr
:
number
[],
k
:
number
)
:
number
{
20
// 定义窗口指针
30
let
left
=
0
;
40
let
right
=
0
;
50
// 定义窗口内元素总和
60
let
sum
=
0
;
70
// 定义最大总和
80
let
max
=
0
;
90
while
(right
<
arr.
length
) {
10
// 移动右边界并更新元素总和
11
sum
+=
arr[right
++
];
12
// 当窗口长度为k时,更新最大总和并移动左边界
13
if
(right
-
left
===
k) {
14
max
=
Math.
max
(max, sum);
15
sum
-=
arr[left];
16
left
++
;
17
}
18
}
19
return
max;
20
}
总结,窗口从小变大到 K,然后就在逻辑上固定窗口 大小,先后移动右左边界,直到右边界到达数组末尾。
二、思考题
我们在上面这个题目的基础之上,新增一个条件:
题目描述
给你一个整数数组 nums
和一个整数 k
。请你从 nums
中满足下述条件的全部子数组中找出最大子数组和:
- 子数组的长度是 k,且
- 子数组中的所有元素 各不相同 。
返回满足题面要求的最大子数组和。如果不存在子数组满足这些条件,返回 0 。
子数组 是数组中一段连续非空的元素序列。